Product Design: Finding New Concepts With CK Theory
Explore the unknown and develop new concepts using CK theory.

Design can be approached in so many ways. Tools and frameworks will be suggested to you in order to determine what roadmap you should follow, what steps you should take… But what we do not talk enough about is what happens at the very start when yourself attempt to generate, innovative concepts, when you require this ability to “think out of the box” in order to create something new.
This is why I would like to offer you an introduction to a theory that not only focuses on design, but also seeks to help you build and develop new, innovative concepts, or concepts which did not exist beforehand.
CK Theory Defined
The CK theory is a unified design theory developed by a renowned school in France called Les Mines ParisTech. It was introduced by Hatchuel and Weil in 1996, further expanded by Le Masson’s work. All three are professors at Les Mines. Since then, major French companies have incorporated it into their research and innovation efforts.
The purpose of CK theory is to formalise design reasoning, or exploration into the “unknown”. It provides a model for the design process of a desirable but partially unknown “object”, considered undecidable at time t - because it does not yet exist-, given initially available knowledge (Le Masson et al., 2017).
Innovative design : the process of working towards something which does not yet exist.
C and K represent two distinct spaces. C stands for concept space, or a space where conceptualisation happens. K stands for knowledge space. Think of it as space where you have islands, each island inhabited by knowledge on a specific topic. Together, these islands constitute an archipelago - might as well go all the way with the metaphor-, which constitutes our knowledge base.
The CK theory model relies on the relationship between these two spaces. The design process is in a large sense a formalization of a back-and-forth between the two, which ultimately helps you develop new concepts.
Here is an example of how C and K interact. If our goal for example is to design a new concept, something which does not yet exist, such as a “sustainable fridge”, we will use the knowledge we have on “sustainability” and “fridges” - located in K-space-, in order to develop this new concept in C-space. This process will allow us to design a “sustainable fridge”. Once we have designed one, it is no longer something “unknown”. Now that it exists, it becomes knowledge which will enrich the initial knowledge we had. This is in broad terms how we can describe the design process using CK theory.
We provide below a more in-depth description of the fundamentals of CK theory.
Main Notions
Starting Point
In CK theory, the starting point is an “unknown”, or a proposition which is interpretable thanks to currently available knowledge and yet “undecidable” still (ex: modern chair, mass consumption product without packaging...etc) (Le Masson & McMahon, 2016). You cannot This “unknown” is the concept we are reaching for in the CK model.
Knowledge Space
In K-space, we have propositions which have a logical status, meaning that they are each either true or false. K propositions can be tacit or explicit, scientific, or based on beliefs. They remain true or false propositions which can be used to work on concepts. These propositions constitute a knowledge based which will be used to act on “things” which are yet “unknown”. K can be considered in the largest sense and cover all topics on which we have established knowledge. K is not static and evolves in time as we keep on discovering new things and come back on what was previously established to adjust our knowledge base of the world available to us (Le Masson & McMahon, 2016).
Concept Space
In C-space, we have propositions with which we can start a work of design. In contrast to K proposition, C propositions do not have a logical status: when C proposition is formulated, it is a priori impossible to find it as either true or false in K. For example, a C proposition could be “a chair without legs” or a “smart grocery basket”. Although C does not belong in K-space (does not have logical status), it should be interpretable or comprehensible using the propositions in K. C-space has an arborescent structure. Expansive reasoning will provide a complex yet organized and structure design activity (Le Masson & McMahon, 2016).
Operators
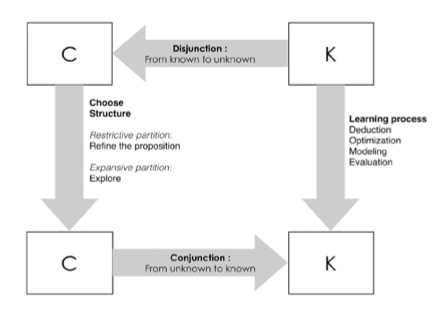
A central mechanism of design is the process of adding and subtracting properties to concepts or propositions, whereby we transform propositions in K into concepts of C and vice versa. In transforming K and C, we use four operators (external operators: C→K, K→C; internal operators: C→C, K→K), composing what we call the “design square”. This “design square” reflects the dual dynamics of design in CK theory: disjunction and conjunction. Here are descriptions for each operator as provided by Agogué, Hooge and Arnaux (2014):
K→C: This operator adds/removes properties from K to concepts in C. It creates disjunctions when it transforms a proposition (in K) into a concept (in C). This corresponds to what is usually called “generation of alternatives”, yet concepts are not alternatives but potential seeds for alternatives. This operator allows the partitioning of an initial concept, expanding C-space with elements from K-space.
C→K: This operator represents conjunction. The operator looks for properties in K which could be added/removed to reach propositions with a logical status. Conjunctions can create what we call “finished designs”. When a conjunction happens (i.e., when a concept becomes a proposition with a logical status), the design process stops. When there is no conjunction, there is development of new knowledge and new concepts. Here concepts are prototyped, creating new knowledge.
C→C: This operator is based on traditional rules of set theory to make partitions. A partition may be expansive or restrictive (Garel, Mock et al., 2016):
Restrictive partition refers to the division of a finite space according to criteria of choice or a set of given rules. For example, you could easily divide movies available at your home cinema according to genre or duration. Restrictive expansion reduces the space of possibilities without changing the definition or attributes of the object to be designed.
Expansive partition refers to building something new within an initial space, which involves bringing new properties and defining “things” which did not exist at the beginning of the reasoning. An expansive partition changes the identity of the object by adding unexpected attributes to the original concept. It is precisely because of these expansions that breakthrough innovations are possible.
K → K: This operator refers to traditional reasoning, including optimization, deduction, inference, modelisation. It is based on the classical rules of logic and propositional calculus. This operator is used to describe actions to increase the reliability of the proposals in K.
Overall, from the set of possibilities opened by the initial concept, properties will be added or subtracted, partitioning the initial concept. The nature of the different partitions at hand (restrictive vs expansive) will reflect the degree of innovativeness of the design process.
The “Flying Boat” Example
Let’s assume we want to design a “flying boat”. We might already have a variety of boats in the knowledge base, but none have the property of “flying”. However, no fundamental principle asserts that a boat can never have the property of “flying”, hence we cannot say that the proposal “a flying boat” is false. So, the proposal at hand does not have a logical status. The knowledge structure is yet clearly identified. We know quite a bit about boats and flying. We hence have C0 and K-space ready to go.
Initially, the goal of our design reasoning is: 1) a gradual addition of attributes in C-space to enrich and extend the definition of the object we want to design (e.g., a flying boat with wings); 2) enrich our knowledge (knowledge on flying can be further view in various ways: wings, inflatable balloon, helicopter etc...). These two expansions are complementary. We note that any expansion in knowledge can also provide new attributes in C-space and vice-versa, adding a property to C- space creates new pockets of knowledge to explore in K-space.

Expansions
In C-space: the aim is to build a tree-like structure starting from the initial concept. An additional attribute either extends a given definition or opens up an alternative design path.
In K-space: each new mobilized pocket of knowledge is added to K-space independently of pre- existing pockets.
Two new attributes have been added in the diagram: one in extension, meaning ‘a flying boat with wings and a thrust provided by a propeller and a rotor” and the other opening of an alternative design path, meaning a “flying boat that flies like a balloon”.
To conclude, we show how new knowledge can open new partition in C-space. For example, while using the “flying” attribute, a search for “flying” in terms of knowledge can bring out a new genre of knowledge say for example on the “flight” of a flying fish. It opens a new path in C-space: a flying boat that flies like a flying fish. The expansions in C-space rely on the structure and content of K-space. Hence, they are K-relative.
Conclusion
This is a rather theoretical presentation. However, let’s not forget that CK theory was meant to have a concrete use. It provides a methodological, actionable approach to design which can be used in a group or a team, brainstorming together to come up with new concepts. Governmental organisations and companies have incorporated the CK method into their innovation practices, including Thales, Schneider Electric, Airbus, Renault, SNCF and RATP. If your team is working on developing a new, innovative concept for a product, the CK method is a great tool!
If you would like more information on CK theory and how it can be applied, click here.
Quote
To innovate is to engage in innovative design activity or to conceive what is yet “unknown”. - Pascal Le Masson
References
Agogué Marine, Hooge, S., Arnoux Frédéric, Brown, I., Hatchuel, A., Weil Benoît, Amar, G., & Trémoureux Carl. (2014). An introduction to innovative design: Elements and applications of C-K Theory. Presses des Mines-Transvalor.
Garel, G., & Mock, E. (2016). La Fabrique de l'innovation: Embarquez pour la Conception Innovante. Dunod.
Le Masson, P., & Mcmahon, C. (2016). Armand Hatchuel et Benoit Weil La Théorie C-k, un fondement Formel aux théories de l'innovation. MINES ParisTech. Retrieved October 1, 2022, from https://hal-mines-paristech.archives-ouvertes.fr/hal-01243331
Le Masson, P., Weil, B., & Hatchuel, A. (2017). Design theory. SpringerLink. Retrieved October 1, 2022, from https://link.springer.com/book/10.1007/978-3-319-50277-9